Contents. For electromagnetism all you need to know is what happens when you have + or – charges, what happens when they get close and what happens when they move. For all of non-quantum EM there are only 5 formulas you need. The 4 Maxwell Equations and the Lorentz equation describe all of electricity, magnetism, light, sound, radiation, actually most of physics: (1) (2) (3) (4) (5) How bad can a topic be if you can describe it all with just 5 equations, you could probably fit them all on the back of a beermat. Now that you’ve seen the conclusion we can go to the beginning and read the whole story in detail. Unless you’re doing a university course you can get away with not knowing exactly what the equation mean or do, but this site will explain them later, first lets get back to basics.
The Basics Charge comes in 2 types, positive and negative and is measured in Coulombs (C). If you have a charge on its own it emits a field in all directions. The field from a charge is represented by E as in E-lectricity. If you put another charge in the field it experiences a force. Like charges repel and unlike charges attract.
Electromagnetic induction, electromagnetism, electronics, fluid dynamics, units. Principles of physical science dsst study guide free, principles of physical science dsst a free study guide. Energy and Electromagnetism Study Guide. Magnetism: • Opposite poles ______; same poles ______. • Magnets stick only to objects made of ______.
The bigger the charge the stronger the force and the further away the charges the weaker the force, exactly what you’d expect. This relationship can be represented by Coulombs Law; and The ‘s are the two charges and is the distance between them squared. The other bit is just a constant which roughly equals. (The exact derivation of this law can be found here). From these you can see that the force is just the field times by whatever charge you put in,. Using this you can work out the field or force between particles or atoms or anything with charge provided they’re not moving.
Once you start a charge moving other things happen. Stuff Moving As soon as a charge starts to move it produces another field. The new field is magnetism and is represented by B as in B-magmatism? The reason it’s B is simply that it was the second thing in an alphabetical list:.
Electromagnetic vector potential: A. Magnetic induction: B. Total electric current: C.
Electric displacement: D. Electromotive force: E. Mechanical force: F. Velocity at a point: G. Magnetic intensity: H (This also explains where H comes from for those interested).
So now your particle or atom or whatever has 2 fields coming out. The full equation to describe how both fields act on a particle is which is known as the Lorentz force.
The symbol does not signify multiplication, in this context it means Cross-Product. It’s basically a short way of writing “ times times the sine of the angle between”. This is because the field pushes at 90° to which ever direction its pointing AND which ever direction you are moving in. Now unless you’re doing EM past A-level you can forget all about the directions and angles and just write If we expand out the above expression we have But we can already describe one of these bits, is just Coulombs Law.
Also, at A-level or below the situation will probably be simplified so you only have to consider the and fields separately. So you will probably only have to use one of the following two formulas, Obviously is the force and is charge, and are the two fields previously described and is the velocity of the moving charge. The electric field is measured in the SI units of Newtons per coulomb ( ) or, equivalently, volts per meter ( ). The magnetic field has the SI units of Teslas (T), equivalent to Webers per square meter ( ) or volt seconds per square meter ( ) Circuits Now I’m not a big fan of circuits, never have been, now hopefully I’ll be professional enough that my disliking of them won’t come across in this section but if it does I apologise in advance. If I really start to struggle with my hate I may have to call in a second writer A circuits is basically just a series of moving charges with the occasional object or device in the way that affects the flow. Now when I say the electrons are moving around most people will think that their speeding around at close to the speed of light, but this is wrong. The actual electrons are moving EXTREMELY slowly, it’s the wave that travels fast.
As stated above like charges repel, so put one electron next to another and they will move apart. With a current in a wire you basically have a tube of electrons and you’re adding one to one of the ends, this causes the next electron to move down which in turn pushed the next one and so on. So you have a Mexican wave like effect that moves quickly, but the electrons themselves are only moving slowly. Circuits usually contain all sorts of different objects and devices depending on what they’re for, and depending on how you set them all up in the circuit depends how you do all of you calculations.
Which is Which? If you set up all your component in a closed loop like so then we say that all the components are in Series.
If you set them up with branching paths like so then we say that the components are in Parallel. You can also make circuits that are a mixture of series and parallel section like so Amps, Volts and Ohms (Oh my!) We call the moving charges a Current, and it is measured in the SI unit of Amps (A). Amps are equivalent to the amount of charge passed in a certain time, so 2 coulombs in 6 seconds will be equivalent to 0.3A.
This, like most things in physics can be expressed in a nice formula for you to learn Another important idea in circuits is Voltage or Potential Difference. Volts are basically the difference in the Electric potential at two different points. The electric potential between 2 points is given as where is the distance between and. It’s basically field times distance. Another important idea when it comes to circuits is resistance. Resistance is basically a measure of how much resistance opposes an electric current.
Almost all objects or devices in a circuit cause resistance and to calculating the total resistance in a circuit you use one or more of these rules One of the most important and fundamental equations in circuits is Ohm’s law, and it relates current, voltage and resistance. The Deep End This is it.
Classical EM goes no deeper than this. These 4 are the fundamental equation for ALL fields in EM. They may take a bit to get your head around but once you do it should all make sense, sort of.
If you don’t know about integration and differentiation I suggest you head over to the Integration section or the Differentiation section, I’ll try to explain it here but I’ll mainly be focusing on the physics. Gauss’ Law Ok then first up we have Gauss’ Law. This says that the integral of the Electric field, through a closed area is equal to the total charge inside of the area, divided. Is a constant called The Permittivity of Free Space and shows up all over physics along with which is The Permeability of Free Space. What this equation means is you can take ANY closed surface you like and find the field going through, provided you can do the maths. Usually you can’t.
However there are a number of cases when its nice and easy. Cases when the field is coming straight out through the surface evenly. The cases are. A Spherical surface around a point or sphere.
A Cylindrical surface around an infinite wire. A Regular surface over a section of an infinite plane I admit these sound vague and abstract so I will demonstrate with the aid of a diagram. These are the Gaussian surfaces. Basically with these surfaces all you’re trying to do is make life easier. You just make sure that the surface is always the same distance from the charge source and that the field is always going through at 90 degrees. You can then work out the integral with your eyes closed its that easy. The left hand side of Gauss’ law becomes E times the surface of the shape you chose.
A Spherical surface becomes, where is the radius of the sphere. A Cylindrical surface becomes, where and are the length and radius of the cylinder. A Regular surface becomes, where is the Area above and below the infinite surface (you need the factor of 2 as the field goes above and below the surface at 90 degree).
So Gauss’ law for a sphere becomes Which was introduces earlier as Coulombs Law, now you know where it came from. Gauss’ Law for an infinite line of charge is just Now in this something new has been introduced,. If you have an infinite line of charge then the total charge on it is infinite and there is no way of knowing how much of that infinite charge you would have inside your gaussian surface. That’s where comes in, its a value of charge per unit length, so if =4Cm and you have 5 metres then the charge is just 20C.
That’s all is, just a value of charge. For an infinite surface gauss’ law becomes Once again a new symbol has been added but its just like the one before. Is just the charge per unit area, so if =5Cm and you have a 100m area the total charge is 500C. Charged Ring Lets say you’ve got a charged ring and you need to know the field produced from it. Once again we’ll be employing one of the most important tools in physics, making stuff easier.

Firstly we’ll only look at the field along the axis of the ring, otherwise things just get too complicated and it’s not worth the effort. Now lets just take a very small part of the ring and say that it’s a sphere.
This isn’t really true, but the smaller we make the section the more we can make it resemble a point charge. So you have something like this You want to find the field at a point along the axis from the ring of total charge and radius.
The little square section at the top, that’s the bit that you assume is a charged sphere. Now we don’t know how much charge is in that little section as you can make it any size you want so we just call the charge, a small amount of. So we now have.
Now if you think about it, every bit of the ring above the axis pushing down will have an equal bit below the axis pushing up. It’ll also be the same for left and right and all other parts of the ring. So all the force from the ring will only be acting along the axis. To work out only this bit we need to use some trig. We need to times the field by to get the axial component. As you may or may not know can also be described (using SOH CAH TOA) by the following relationship for our situation As is the adjacent side and is the hypotenuse. So now we have However we may not know what is.
We do know the radius of the disk, and the distance we are from the disk,. Using a bit of the old Pythagoras we can rewrite in terms of and So now our equation looks like this Now we want to get rid of that, so we integrate Now we know from the diagram at the start that the total charge on the disk is, so if we add up all the little bits of the total should be, so the integral is just.
The physics of the universe appears to be dominated by the effects of four fundamental forces: gravity, electromagnetism, weak nuclear forces, and strong nuclear forces. These forces control how matter, energy, space, and time interact to produce our physical world.
All other forces, such as the force you exert in standing up, are ultimately derived from these fundamental forces. We have direct daily experience with two of these forces: gravity and electromagnetism. Consider, for example, the everyday sight of a person sitting on a chair. The force holding the person on the chair is gravitational, and that gravitational force balances with material forces that 'push up' to keep the individual in place.
These forces are the direct result of electromagnetic forces on the nanoscale. On a larger stage, gravity holds the celestial bodies in their orbits, while we see the universe by the electromagnetic radiation (light, for example) with which it is filled. The electromagnetic force also makes possible the advanced technology that forms much of the basis for our civilization. Televisions, computers, smartphones, microwave ovens, and even the humble light bulb are made possible by control of electromagnetism.
The average physics major will spend more time understanding and applying the concept of electromagnetic force than he or she will spend studying any other type of force. The classical (i.e., non-quantum) theory of electromagnetism was first published by James Clerk Maxwell in his 1873 textbook A Treatise on Electricity and Magnetism. A host of scientists during the nineteenth century carried out the work that ultimately led to Maxwell's electromagnetism equations, which is still considered one of the triumphs of classical physics. Maxwell's description of electromagnetism, which demonstrates that electricity and magnetism are different aspects of a unified electromagnetic field, holds true today. In fact, Maxwell's equations are consistent with relativity, which was not theorized until 30 years after Maxwell completed his equations. In this course, we will first learn about waves and oscillations in extended objects using the classical mechanics that we learned about in.
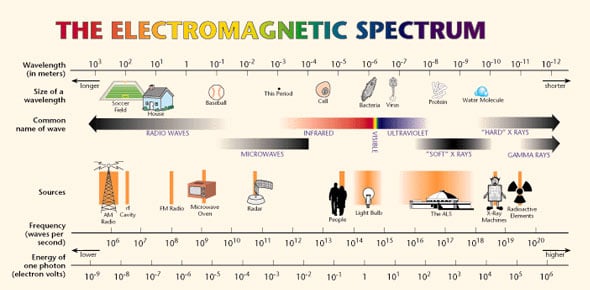
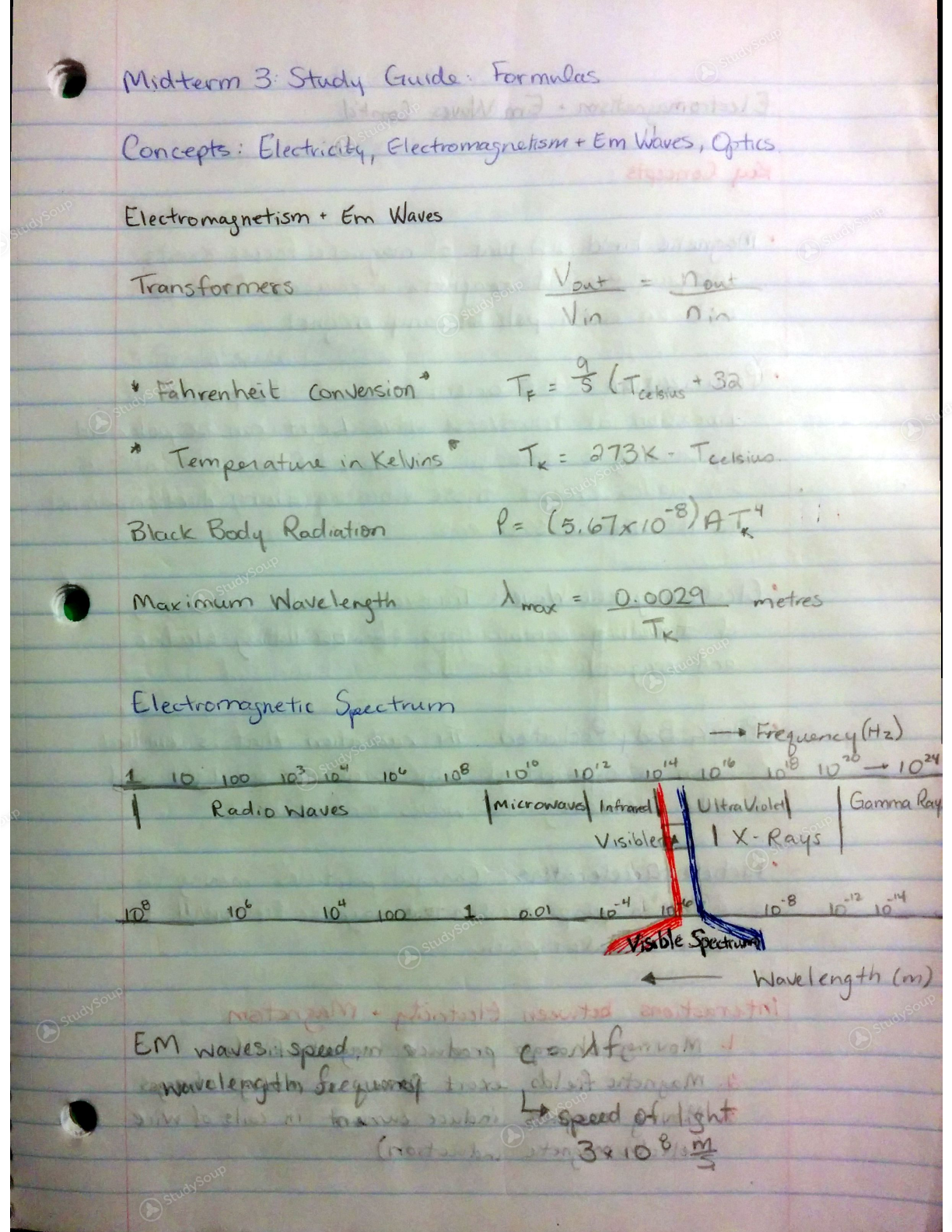
We will also establish the sources and laws that govern static electricity and magnetism. A brief look at electrical measurements and circuits will help us understand how electromagnetic effects are observed, measured, and applied. We will then see how Maxwell's equations unify electric and magnetic effects and how the solutions to Maxwell's equations describe electromagnetic radiation, which will serve as the basis for understanding all electromagnetic radiation, from very low frequency, long wavelength radio waves to the most powerful astrophysical gamma rays. We will briefly study optics, using practical models largely consistent with the predictions of Maxwell's equations but that are easier to use. Finally, this course provides a brief overview of Einstein's theory of special relativity. We will assume that you have a basic knowledge of calculus. This course will require you to complete a number of problems.
Unlike mechanics, most of the phenomena encountered in the field of electromagnetism are not found in everyday experience - at least, not in a form that makes the actual nature of the phenomena clear. As a result, learning electromagnetism involves developing intuition about a rather unintuitive area of physics. In the end, developing physical intuition is less about getting a right answer than it is about getting a wrong answer and then understanding why it is wrong.
In an ideal situation, this course would require you to both work out problems concerning the phenomena and observe various important phenomena in the laboratory. However, because this is an online course, we do not have the luxury of lab sessions. We have included a number of interactive demonstrations to compensate for this.
When you approach a problem, try to work out the size of those quantities that clarify the basic nature of the question proposed. Thinking of these numbers as data from an ideal laboratory will help you develop a sense of how electromagnetism works – a sense that most people do not get from the mathematical description of the physics. After familiarizing yourself with the following course syllabus, enroll in this course using the 'Enroll me in this course” button. Once enrolled, navigate to Unit 1 of the course to read the Unit Introduction and Unit 1 Learning Outcomes. Links and instructions for all unit specific course resources will follow the introductory materials.
In PHYS101, we learned how to describe the motion of particle-like masses using classical mechanics. We will start PHYS102 by examining how objects of size – length, width, depth – behave. We will focus on vibrating systems and the propagation of mechanical waves through media; think of ripples traveling outward from a stone dropped into water. This course will also lay the basic foundation for the development of a classical theory of mechanics for extended solids. Completing this unit should take you approximately 7 hours.
We are now beginning our study of electricity and magnetism. We will discover that electricity and magnetism are two different aspects of the same phenomenon, which is usually referred to as electromagnetism. Our starting place will be electrostatics or, more simply, the rules governing the behavior of static charges. The first experiments on electrical phenomena were carried out by our friend from PHYS101, Thales of Miletus. He observed that one could generate a static charge on amber by rubbing it with wool. Completing this unit should take you approximately 20 hours. Although the study of electric and magnetic fields is interesting in and of itself, it may not seem directly useful in the real world.
However, the interplay between these phenomena is responsible for much of the technology you see in your everyday life. For example, all electronics apply various features of electromagnetism, so that computers, HDTV, iMacs and iPads, smartphones, motors, fans, lights, and so on are applied electromagnetic devices. In this unit, we will take a quick look at the foundations of electronics, while at the same time adding to our understanding of electromagnetism.
Completing this unit should take you approximately 8 hours. Earlier, we studied electric charges, potentials, and fields.
We will now take a look at an important effect of moving charges: magnetism. Thales of Miletus set the stage for the scientific exploration of magnetism back in Ancient Greek times, when magnetism could only be observed via the behavior of natural magnets, called lodestones.
Hans Christian Oersted first noted the relationship between moving electric charges and magnetism much later, when he accidentally discovered that an electric current could deflect a nearby compass needle in 1820. Forty-five years after Oersted made this observation, James Clerk Maxwell united electrical and magnetic phenomena into four reasonably simple equations known since as Maxwell's Equations. Completing this unit should take you approximately 7 hours.
You learned that stationary electric charges produce electric field, and moving electric charges (that is, electric current) produce magnetic field. In this unit, you will find out that the reverse is also true: changing magnetic flux produces electric field, or induces electric current. This is the phenomenon of the electromagnetic induction, which is a basic principles in such devices as generators of electric power, electric motors, and transformers. Completing this unit should take you approximately 13 hours. At this point in the course, we have developed the mathematical structure for and a general understanding of all of Maxwell's Equations. Now we want to sit back and summarize our findings by identifying what they are, what they mean, and how we can use them. There are four Maxwell equations that describe all classical electromagnetism.
Maxwell's equations take on a particularly simple form when describing the behavior of electric and magnetic fields in regions devoid of matter; that is, in a vacuum. (Note that for most purposes, air is close enough to being a vacuum that the presence of an atmosphere can be ignored.) These are Maxwell's free space equations.
There are four Maxwell free space equations. These include the two flux equations - the electric and magnetic forms of Gauss' law.
These state that the electric or magnetic flux through a closed surface is proportional to the electric or magnetic charge enclosed within that surface. Note that in the magnetic case, there are no magnetic charges (also called magnetic monopoles), so that the magnetic flux through and closed surface is zero. The other two free space Maxwell's equations are Faraday's Law of Induction and a modified version of Ampere's Circuital Law. Once again, these electric and magnetic equations have similar formalisms, thereby emphasizing the close relationship of the electric and magnetic fields. Faraday's Law of Induction states that the induced EMF in any closed circuit is proportional to the time rate of change of the magnetic flux through the circuit, while Ampere's Law states that the integrated magnetic field around a closed curve is proportional to the currents passing through a surface bounded by the curve. Maxwell's main contribution (beyond realizing that these four equations provided a complete theory of electromagnetism) was the discovery and description of the displacement current, which is a source of the magnetic field associated with the rate of change of the electric displacement field in a region. Inside materials, Maxwell's Equations are modified by the electric permittivity and magnetic permeability of the materials, but they remain the basis for the classical model of electromagnetism.
In this unit, we will concentrate on Maxwell's Equations as a single theory that unites the half-century of previous work on electromagnetism. Completing this unit should take you approximately 8 hours. An optical phenomenon involves the interaction between electromagnetic waves and matter. We will focus on visible, infrared, and ultraviolet light, but much of the study of optics will apply to some extent to radio waves and x-rays. The complete study of optics involves enormously complex mathematics, a thorough understanding of both classical and quantum optical effects, and a great deal of ingenuity for success.
For the purposes of this course, optics will be limited to the classical description of electromagnetism provided by Maxwell's equations: the full wave optics. Even this level of description is quite complicated for most optical phenomena, so we will apply simplified models to develop a basic understanding of how optics works. In geometric optics, we assume that all light travels in straight lines. In paraxial optics, we assume that all optical systems handle light rays near a symmetry axis of the optical system, which allows us to largely ignore aberration, a vast array of terribly complex optical effects. Completing this unit should take you approximately 11 hours. The physical descriptions we have studied to this point were based on a notion of absolute space and time.
Study Guide Electromagnetism
A model for this point of view was that space is filled everywhere by a continuous medium called the ether. Light and other forms of electromagnetic radiation were waves in this ether, analogous to sound waves in air. All other phenomena were to be understood as various manifestations of Maxwell's electromagnetism, which was originally based on a mechanical model of ether. It seemed reasonable that the 19th Century 'theory of everything' could be tied down by measuring the 'elastic' properties of the ether. Toward the end of the 1800s, however, this model became associated with more and more hastily patched cracks. The detailed history of the gradual realization that ether models were not quite right is complex and technical. However, there is one rather clear indication of trouble.
Chapter 26 Study Guide Electromagnetism
In 1887, Albert Michelson and Edmund Morley of the Case Institute (now Case Western University) performed an experiment using an optical interferometer in which they compared the speed of light in two beams traveling at right angles to each other. If the speed of light relative to the ether was always the same, the measured speed of light would be larger or smaller depending on the direction the experiment was traveling through the ether. The motion of the Michelson-Morley experiment was provided by the rotation of the Earth on its axis and the orbital motion of the Earth around the Sun, as well as the absolute velocity (if any) of the Sun relative to the ether.
Study Guide Electromagnetism Pdf
They expected to see both diurnal changes and yearly changes in the relative velocities of light in the two paths. True, the changes expected by classical ether theory were small (on the order of 0.01% of the velocity of light), but the Michelson-Morley interferometer was able to detect velocity changes about 6-7 times smaller. To the surprise of all, there were no changes whatever observed. This experiment was widely repeated, using constantly improving equipment - a new version of the experiment carried out in 2002 established that the velocity of light is constant to better than 1 part in 1015 - one of the most precise physical measurements ever accomplished. The explanation of the Michelson-Morley null result was length contraction, as developed by Hendrik Lorentz and George Francis FitzGerald. Length contraction explained the Michelson-Morley result, the idea being that matter is held together by electromagnetic forces (true), and so the actual size of objects will change with motion through the ether (false). In the end, it was Albert Einstein's formulation of the theory of Special Relativity that gave us a consistent explanation of all such phenomena.
His primary postulate was to accept that the speed of light and the laws of physics are constant in all reference frames – including reference frames that are in motion. Oddly, despite the fact that Einstein's theory completely explained the Michelson-Morley result, he took no motivation for his theory from that experiment.
Completing this unit should take you approximately 10 hours. These study guides are intended to help reinforce key concepts in each unit in preparation for the final exam. Each unit study guide aligns with course outcomes and provides a summary of the core competencies and a list of vocabulary terms. The study guides are not meant to replace the readings and videos that make up the course. The vocabulary lists include some terms that might help you answer some of the review items, and some terms you should be familiar with to be successful in completing the final exam for the course.